В мире вычислительных наук существует задача обработки и преобразования логических выражений. Одной из важных задач в этом контексте является преобразование сложной дизъюнктивной нормальной формы в конъюнктивную нормальную форму, что позволяет упростить выражение и дать более наглядное представление о его логической структуре.
Этот процесс требует четкого понимания и правильного выбора методов и подходов, чтобы достичь наилучших результатов в эффективности и точности. В данной статье мы представим несколько стратегий, которые существенно облегчат задачу преобразования, а также рассмотрим некоторые рекомендации и инструкции для выполнения этого процесса.
Во-первых, необходимо акцентировать внимание на значимости правильного выбора методов преобразования. Множество подходов к этой задаче позволяют выбрать наиболее подходящий вариант в соответствии с особенностями исходного выражения. Некоторые из таких методов включают алгоритмы редукции, логические эквивалентности и применение алгебраических свойств. Важно уметь определить, какой метод будет наиболее эффективным в данной ситуации, чтобы достичь наилучших результатов.
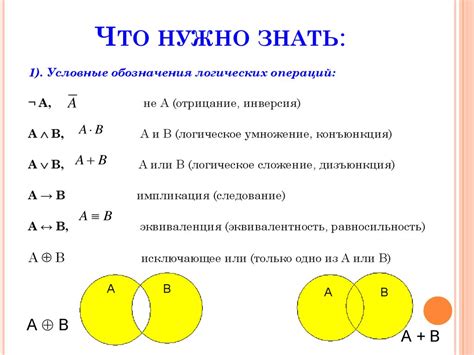
Что такое СДНФ и КНФ?

СДНФ - это одно из основных представлений булевой функции. Она позволяет описать функцию в виде конъюнкции, то есть логического "И" от нескольких переменных или их отрицаний. СДНФ может быть использована для описания любой булевой функции и представляет собой набор дизъюнкций, объединенных логическим "ИЛИ". Таким образом, СДНФ позволяет представить функцию в конъюнктивной нормальной форме.
КНФ - это другой формат представления булевой функции. Она представляет функцию в виде дизъюнкции, то есть логического "ИЛИ" от нескольких конъюнкций переменных или их отрицаний. КНФ также является одним из важных способов представления булевых функций и может быть использована для описания любой функции в дизъюнктивной нормальной форме.
Знание и понимание СДНФ и КНФ является важным шагом в освоении темы "Преобразование СДНФ в КНФ". Они представляют собой основные форматы, в которых можно представить булевые функции, и позволяют исследовать и изменять их с разных сторон. Поэтому в дальнейшем будем рассматривать различные методы и техники преобразования функций из СДНФ в КНФ с использованием эффективных алгоритмов и инструкций.
Почему стоит применять трансформацию СДНФ в КНФ?

Путем упрощения и структуризации исходного выражения, преобразование СДНФ в КНФ обеспечивает лучшую читаемость кода и более эффективное выполнение вычислений. Уникальная комбинация конъюнкций и дизъюнкций в КНФ позволяет сократить объем информации и упростить логические связи между переменными.
Пользуясь данным методом, можно существенно упростить анализ и проектирование сложных систем, таких как электронные схемы, базы данных или логические алгоритмы. Преобразование СДНФ в КНФ дает возможность лучшего контроля над процессом вычислений и позволяет создать более компактный и эффективный код.
Преобразование СДНФ в КНФ: стратегии и подходы

В данном разделе мы рассмотрим различные стратегии и подходы к преобразованию СДНФ (сокращенной дизъюнктивной нормальной формы) в КНФ (конъюнктивную нормальную форму). В связи с необходимостью преобразования логических выражений из одного представления в другое, существует несколько оптимальных методов для достижения данной задачи.
Манипуляции с отрицанием
- Использование законов двойного отрицания
- Применение законов де Моргана
- Упрощение логических операндов с помощью алгебры Буля
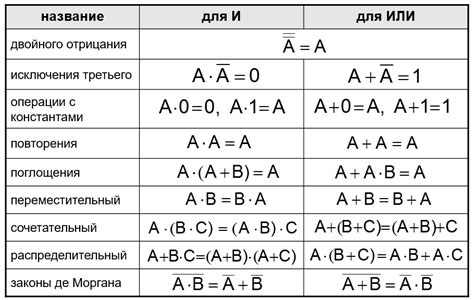
Для преобразования СДНФ в КНФ эффективно применять различные манипуляции с отрицанием, такие как использование законов двойного отрицания или применение законов де Моргана. Эти методы позволяют перегруппировать и упростить логические операнды, в результате чего достигается искомая КНФ. Дополнительно, алгебра Буля может использоваться для упрощения логических выражений и достижения более компактного представления в КНФ.
Метод склеивания
- Склеивание с одинаковыми дизъюнктами
- Склеивание с дополнением
Метод склеивания является одним из эффективных подходов к преобразованию СДНФ в КНФ. Он позволяет объединить дизъюнкты с одинаковыми переменными или переменными, образующими дополнение друг друга. При использовании такого метода можно значительно сократить количество логических операций, что упрощает итоговую КНФ.
Равносильные преобразования
- Замена тождественной и фиктивной переменных
- Ассоциативность логических операций
- Коммутативность логических операций
Для эффективного преобразования СДНФ в КНФ можно использовать равносильные преобразования, которые позволяют заменить тождественные и фиктивные переменные, а также изменить порядок и группировку логических операций. Эти преобразования основаны на ассоциативности и коммутативности логических операций, и позволяют достичь более оптимальной КНФ.
Метод раскрытия скобок

Как правило, формулы в СДНФ имеют вид конъюнкции логических выражений, в которых каждое выражение является дизъюнкцией литералов или их отрицаний. Для преобразования данной формулы в КНФ необходимо раскрыть скобки, упростив тем самым логическое выражение.
Раскрытие скобок осуществляется путем применения законов дистрибутивности, ассоциативности и других логических преобразований. Это позволяет преобразовать сложную комбинацию логических операций в более простую и понятную форму.
Применение метода раскрытия скобок может значительно сократить количество логических операций и упростить формулу до самой компактной формы КНФ. Благодаря этому методу можно получить более эффективное представление логических выражений, что является важным для многих областей, включая формальную логику, криптографию и автоматизацию решения логических задач.
Метод упрощения отрицаний

В данном разделе рассмотрим стратегии и способы упрощения отрицаний логических выражений, которые позволяют существенно улучшить эффективность преобразования формулы из СДНФ (совершенной дизъюнктивной нормальной формы) в КНФ (конъюнктивную нормальную форму). Такой подход основывается на избавлении от двойных отрицаний и приведении негационных операций к конкретным законам логики и алгоритмам упрощения, что позволяет сократить сложность и размер исходной формулы.
Раздел будет посвящен рассмотрению основных техник, включающих использование законов де Моргана, законов ассоциативности и дистрибутивности, а также применение правил отрицания двойных отрицаний, правил редукции, логической эквивалентности и других методов упрощения выражений.
Описанные методы позволяют значительно упростить логическое выражение, устранить избыточность и повысить его читаемость, что является важным шагом перед преобразованием формулы из СДНФ в КНФ. Кроме того, применение этих методов обеспечивает возможность выявить и устранить логические ошибки или нестабильные участки в исходном выражении, что повышает надежность и корректность результата преобразования.
Метод упрощения одинаковых конъюнкций в процессе преобразования формы дизъюнктивной нормальной формы (ДНФ) в форму конъюнктивной нормальной формы (КНФ)

В данном разделе мы рассмотрим метод упрощения одинаковых конъюнкций в процессе преобразования формулы из ДНФ в КНФ. Этот метод позволяет минимизировать количество повторяющихся конъюнкций в итоговой формуле и повысить эффективность преобразования.
Метод состоит в определении и удалении конъюнкций, которые уже встречались в предыдущих частях формулы. При преобразовании формулы из ДНФ в КНФ, мы стремимся к получению максимально упрощенной и компактной формулы, поэтому исключение одинаковых конъюнкций является важным этапом процесса.
Для применения данного метода, необходимо провести анализ формулы и выделить повторяющиеся конъюнкции. Затем, используя знания о свойствах конъюнкции, мы можем заменить повторяющиеся конъюнкции одним эквивалентным выражением. Таким образом, мы сокращаем количество конъюнкций в итоговой формуле, что способствует ее упрощению и более эффективному представлению в КНФ.
Применение метода сокращения одинаковых конъюнкций является значимым в процессе преобразования формы ДНФ в КНФ, поскольку позволяет улучшить читаемость и понимание формулы, а также повысить ее эффективность при выполнении логических операций. Оптимальное использование этого метода требует глубокого понимания логических операций и свойств конъюнкции, что помогает преобразовать формулу таким образом, чтобы сохранить ее истинность и компактность.
Как преобразовать логическое выражение в другую форму
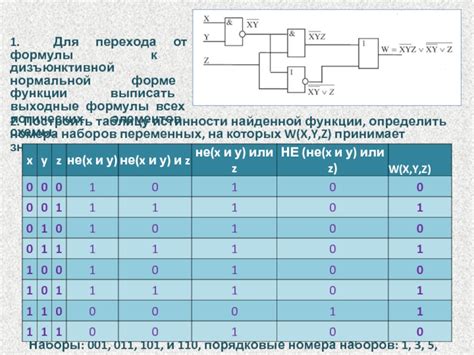
В данном разделе мы рассмотрим подробные инструкции по преобразованию логического выражения из СДНФ в КНФ. Перед нами стоит задача изменить структуру логической формулы, чтобы она соответствовала производным нормальной форме. Мы избегнем использования сложных методов и сконцентрируемся на простых шагах, которые помогут вам осуществить это преобразование.
Прежде всего, мы предлагаем вам разбить логическое выражение на отдельные конъюнкции. Затем мы проанализируем каждую конъюнкцию по отдельности и будем применять определенные операции. Наша цель - создать конъюнкцию, которая будет содержать только простые литералы или их отрицания.
Одним из вариантов преобразования логического выражения является использование законов де Моргана. Эти законы позволяют нам изменить структуру выражения, заменив конъюнкцию на дизъюнкцию или наоборот, а также инвертировав все литералы выражения.
Кроме того, инструкции по преобразованию логического выражения из СДНФ в КНФ будут включать рассмотрение случаев, когда в выражении присутствуют отрицания. Мы дадим вам советы, как разложить сложные отрицания на простые элементы и превратить их в литералы. Это позволит нам создать КНФ, где каждый литерал будет являться простым истинным или ложным утверждением.
| Преобразование | Пример |
|---|---|
| Закон де Моргана | (A∨B)' = A'∧B' |
| Разложение отрицания | ¬(A∧B) = A'∨B' |
После выполнения этих шагов вы сможете преобразовать логическое выражение из СДНФ в КНФ. Мы надеемся, что инструкции и советы, представленные в данном разделе, помогут вам освоить этот процесс и применить его в практических задачах.
Шаг 1: Подготовка формулы для создания нормальной дизъюнктивной формы
Во время подготовки формулы обратите внимание на ключевые элементы, которые может быть удобно выделить и обозначить с помощью синонимов или выделения текста жирным или курсивом. Например, можно выделить логические операторы, логические переменные или константы, а также выделить подформулы, которые являются основой для дальнейшего преобразования.
Важно отметить, что на этом шаге не выполняется непосредственное преобразование формулы в нормальную конъюнктивную форму, но подготовка формулы СДНФ позволит более эффективно выполнить последующие этапы преобразования и достичь желаемого результата.
Шаг 2: Раскрытие скобок

Раскрытие скобок - процесс, при котором мы заменяем группы выражений в скобках их эквивалентными выражениями без скобок. Это позволяет упростить и улучшить читаемость логического выражения. Например, вместо "A ∧ (B ∨ C)" мы можем написать "A ∧ B ∨ A ∧ C", что делает структуру выражения более понятной и компактной.
Для раскрытия скобок в логических выражениях мы используем логические законы и правила, которые определяют эквивалентные преобразования. Некоторые из таких правил включают дистрибутивность, ассоциативность и коммутативность операций. Мы можем применять эти правила последовательно для раскрытия скобок и достижения нужной формы выражения.
Раскрытие скобок позволяет сделать логические выражения более понятными и упрощает их дальнейший анализ и преобразование. В следующем разделе мы рассмотрим методы и примеры раскрытия скобок, а также оптимальные стратегии, позволяющие достичь наилучших результатов в преобразовании сднф в кнф.
Шаг 3: Сокращение отрицательных значений

В данном разделе мы будем изучать методы оптимизации представления логической формулы путем сокращения отрицательных значений, что позволяет упростить ее структуру и сделать ее более понятной для анализа и анализа.
В процессе сокращения отрицаний мы будем обращаться к различным стратегиям, которые позволяют нам упростить формулу без изменения ее смысла. Мы будем использовать разные приемы и методы, чтобы минимизировать количество отрицаний и сделать код более читаемым и легким для дальнейшего анализа.
Для достижения этой цели мы будем применять различные преобразования, включая логические свойства и законы, которые позволяют нам упростить формулу и сделать ее более компактной. Мы также рассмотрим специальные паттерны и практические советы, которые помогут нам эффективно сократить отрицательные значения и улучшить качество нашей формулы.
Шаг 4: Упрощение одинаковых сочетаний логических элементов
На этом этапе мы приступаем к оптимизации полученной КНФ-формулы путем удаления одинаковых конъюнкций. Этот процесс заключается в идентификации и объединении конъюнкций, которые эквивалентны друг другу и не несут новой информации.
Для выполнения этого шага мы применяем метод анализа и сравнения каждой конъюнкции с остальными, чтобы определить, существуют ли одинаковые сочетания логических элементов. Если мы находим одинаковые конъюнкции, мы объединяем их в одну конъюнкцию, удаляя повторяющиеся элементы.
Это позволяет существенно уменьшить размер КНФ-формулы и повысить ее эффективность. Упрощение одинаковых конъюнкций является важной частью процесса преобразования СДНФ в КНФ, так как позволяет получить более компактную и логически эквивалентную формулу.
В таблице ниже приведены примеры сокращения одинаковых конъюнкций:
| Исходная конъюнкция | Упрощенная конъюнкция |
|---|---|
| (A ∧ B ∧ C) ∧ D | (A ∧ B ∧ C) ∧ D |
| (A ∧ B) ∧ C ∧ D | (A ∧ B) ∧ C ∧ D |
| (A ∧ C) ∧ B ∧ D | (A ∧ C) ∧ B ∧ D |
Мы проводим этот процесс до тех пор, пока все одинаковые конъюнкции не будут объединены и упрощены. В результате мы получаем оптимизированную КНФ-формулу, которая содержит минимальное количество конъюнкций, несущих полезную информацию.
Вопрос-ответ

Что такое СДНФ и КНФ?
СДНФ (совершенная дизъюнктивная нормальная форма) и КНФ (каноническая нормальная форма) - это два важных понятия в логике и информатике. СДНФ представляет собой логическую формулу, в которой каждая дизъюнкция является элементарной конъюнкцией переменных или их отрицаний. КНФ, напротив, является формулой, в которой каждая конъюнкция состоит из элементарных дизъюнкций. Одной из задач может быть преобразование формулы из СДНФ в КНФ или наоборот, с целью упростить выражение и улучшить эффективность работы с ним.
Какие методы применяются для преобразования из СДНФ в КНФ?
Существует несколько эффективных методов для преобразования формулы из СДНФ в КНФ. Один из таких методов - закон де Моргана. Он позволяет заменить операции конъюнкции и дизъюнкции между элементарными конъюнкциями и дизъюнкциями переменных или их отрицаний, что приводит к преобразованию из СДНФ в КНФ. Другой метод - использование таблицы истинности, которая позволяет перебрать все возможные комбинации значений переменных и выразить формулу в КНФ. Также существуют алгоритмы, основанные на алгебре булевых функций, которые эффективно преобразуют формулу из СДНФ в КНФ.
Когда следует применять преобразование из СДНФ в КНФ?
Преобразование из СДНФ в КНФ следует применять в случаях, когда необходимо упростить логическое выражение или провести дальнейший анализ формулы. В некоторых случаях, при использовании КНФ, можно снизить сложность вычислений или упростить проверку истинности или ложности формулы. Также, преобразование из СДНФ в КНФ может быть использовано в задачах оптимизации логических схем или минимизации количества элементов в схеме.
В чем заключается суть преобразования СДНФ в КНФ?
Преобразование суммы ДНФ (СДНФ) в конъюнктивную нормальную форму (КНФ) позволяет упростить логическое выражение таким образом, чтобы оно было более компактным и легче анализировалось. СДНФ представляет собой логическую формулу, в которой все возможные комбинации входных переменных, приводящие к истинным значениям, перечислены в виде суммы произведений, а в КНФ формула представляется в виде произведения сумм, где перечислены все комбинации переменных, приводящие к ложным значениям.